Featured Article
Brains
Everest, how do we know how tall it is? photo: wikipedia
How do we know how tall mountains are? Two answers: in modern times GPS measurements can be made to an accuracy of a few centimeters. Before GPS, trigonometry (just like in high school) was used to estimate the height of peaks.
A British Officer surveying in the Himalayan foothills. Hard work, huh? photo: lsu.edu
Not surprisingly, the British, measurers, organizers, and classifiers of everything they could see, took trigonometric measurement and surveying to its highest form during the Great Trigonometric Survey (of India) in the 19th century. The trigonometric method for measuring peak height requires knowing the precise angles of observation and distance to the mountain being measured and to measure these angles a device, known as a theodolite is used. You’ve probably seen surveyors using them, and thought nothing of it, but now you know.
Survey data for Everest and other Himalayan peaks. source: wikipedia
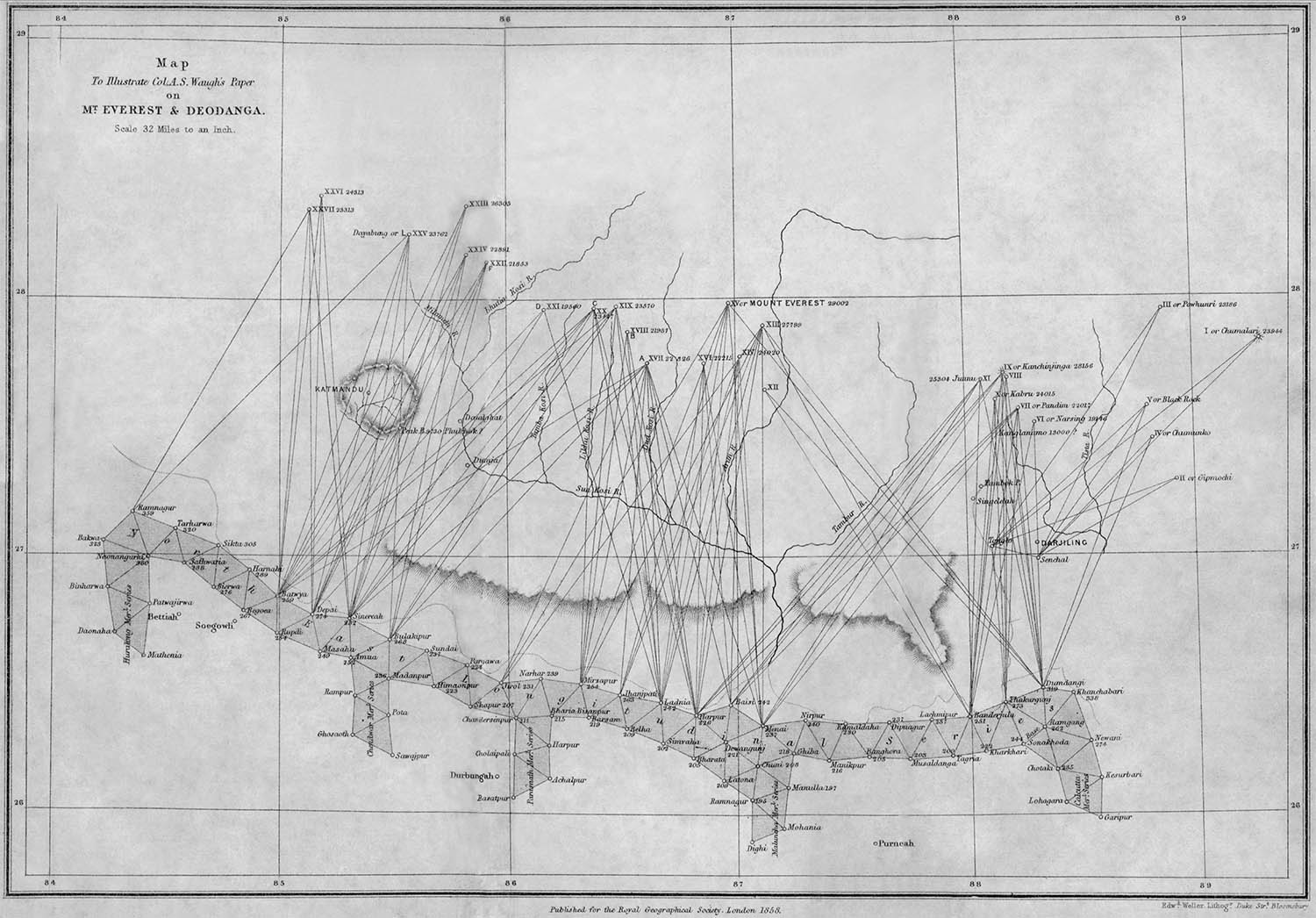
In the early 1800’s the British surveying the Indian Subcontinent (and being British) estimated the height of Mt. Everest to be 29,002 feet tall from 160 miles away. While the trigonometry for measuring mountains uses the same functions (sine, cosine, tangent, and their inverses) as high school trig, the British took it several steps further, incorporating equations to correct for the curvature of the earth, the non-spherical nature of the Earth (more on that), gravitation influence of the mountains on their instruments, atmospheric refraction, and height above sea level.
Explanation of the geoid: 1) ocean 2) ellipsoid (sea level averaged out) 3) local plumb line (pull of gravity) 4) continent 5) geoid (+/- gravity due to differences in ocean height). source: wikipedia
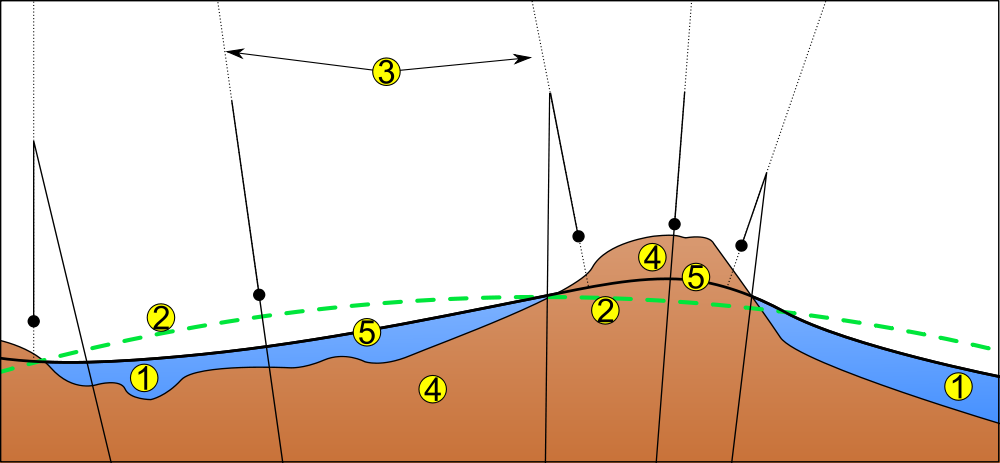
The Great Trigonometric Survey did more than simply measure mountains, it was the first study that measured the geoid nature of Earth. The geoid is the shape of the surface of the oceans under the effect of Earth’s rotation and gravity alone, without the effects of winds or tides. The discovery of the geoid nature of earth was in measuring mountains because the plumb lines, used to measure the local pull of gravity, differ based on location and proximity to mass. Thanks to Newton’s law of universal gravity, we know that gravity is influenced by the mass and proximity of two objects. The shape of the geoid is caused by unequal distribution of density and mass on the Earth’s surface.
To use a theodolite a plumb line, a weight on a string that points towards the gravitational center, is used as a reference from which the angle of distant objects can be measured. That is why it is important the Great Trigonometric Survey account for all the factors that could influence the pull of gravity in a location. Part of this effect is due to the geoid, and the unequal distribution of density and mass on Earth. This causes differences in vertical deflection, differences in the local gravity due to more or less mass in a given location. A theodolite that was not properly oriented and calibrated could skew angle measurements by fractions of degrees; this may not seem like much, but the distances being measured were dozens of miles.
Taking the distance to a peak, measuring the observed angle, and applying the necessary corrections, the British were able to accurately measure mountains. The geoid was also important, because the height of mountains isn’t compared to ‘sea level’ at the nearest beach, but to the geoid surface.
Nowadays, since we pretty much live in the future, we have technology that can measure heights to a margin of centimeters. GPS signals are used to accomplish this; a receiver is placed on top of the mountain, say Mt. Everest. The time it takes for the GPS signal to reach several orbiting satellites is recorded, which indicates the relative elevation from receiver to the satellites. This height is then compared to the geoid, and voila, the height of mountains can be precisely measured. Still, the height of mountains is calculated relative to the geoid. When Mt. Everest was measured by a National Geographic survey using GPS technology in 1999, the height came in 29,035 feet (+/- 6.5 feet), 33 feet off what the British calculated. The circulated height of 29,029 comes from a 1950 Indian survey of the peaks, which the Nepali Government still uses.
That doesn’t solve all arguments. The Tibetans and Chinese currently disagree over whether peaks should be measured to the rock or to the snow on top. For Mt. Everest, this is a difference of some 4 meters. At that point, they’re splitting hairs, but we think it should be with the snow on, because winter is the best season.
